3 月14日は、 円周率３.１４…π（パイ)にかけてπ 日 と呼ばれています。日本ではあまり馴染みがないかもしれませんが、USでは、この日にお菓子のパイを食べたり、無理数である数学の pi（円周率）を計算したりする伝統があります。

Delphiでは、Piは組込み関数のRTLとして提供されています。Systemユニットを見ると、参照はありますが、定義はありません。浮動小数点値は 3.141592653589793238 です (通常、最後の数桁は表示されません)。これはNASAが使用しているものよりも精度が高いのです。しかし理論的な数学やある種の楽しさの定義については、もっとうまくできるはずです。

無理数なので、小数点以下は繰り返されることなく永遠に続きます。 したがって、円周率を計算するときは、精度または桁数の精度を向上させる反復を行います。

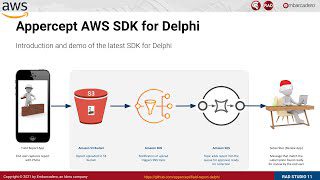
Googleは最近、100兆桁の円周率を計算しました。864 GB の RAM、515 TB のストレージ、82 PB の I/O を備えた 128 個の vCPU のハードウェアスペックで、実に157 日 23時間 31 分 7.651 秒を要したそうです。

このデモンストレーションは、Googleのクラウドコンピューティングのインフラを披露する良い機会でした。したがって私たちは100 兆未満であれば、その計算結果の必要な数字をダウンロードするだけで活用できます。

円周率を計算するとなると、さまざまなアルゴリズムが存在します。数桁の近似値を記憶している方も多いのではないでしょうか。しかし、もっと計算したい場合はどうすればいいのでしょうか？Webを調べ、Wolfram AlphaとChatGPTにも相談しました。ここでは、筆者がまとめたいくつかの例を紹介します。

ライプニッツの公式

マーダヴァの功績で名付けられたこの公式は、およそ14世紀に作られたものです。Delphiでいくつかの例を見つけ、以下のような実装にまとめました。

ただし、この結果は、かなり遅く、不正確なものになります。MaxInt反復で実行すると、3.14159265312413という値になり、小数点以下9桁までしか正確ではありません。

Nilkantha ?

筆者のメモにはNilkanthaと書いてありましたが、詳細は不明です。ライプニッツよりも少し正確だったため、時間を節約できました。

1000回の反復で小数点以下9桁、11000回の反復で小数点以下12桁の精度になります。

もしどなたか別のアルゴリズムを知っている方がいらっしゃいましたら、ご教示ください。

ベイリー＝ボールウェイン＝プラウフの公式

この公式は、1995年にサイモン・プラウフによって発見されました。BBP公式は、先行する桁を計算せずに π の十六進法で n 桁目（二進法で 4n 桁目）の数を直接求めるスピゴット・アルゴリズムを与えます。これをDelphiのコードに変換しようとしたとき、ChatGPTを試してみることにしました。実際に動作するコードに近づくことができ、少しクリーンアップしたコードは以下の通りです。

結果は、非常に高速で、10 桁を表示するだけで十分すぎるほどでした。

Rudy Big Decimal

10桁以上の精度が必要な場合はどうすればいいのでしょうか？

今は亡き偉大な Rudy Velthuis が BigNumbers ライブラリを作成し、GitHubで公開されています。このライブラリにはBigIntegers、BigDecimals、BigRationalsが含まれており、他にも多くの便利なライブラリがあります。BBPアルゴリズムでBigDecimalsを使うように変換したコードは、以下の通りです。

結果は、非常に高速で、非常に長い数字を出力してくれるのですが、残念ながらまだ20桁程度しか正確に取得できませんでした。

まとめ

Delphiで提供しているpi関数はとても実用的ですが、Delphiでゼロから pi を生成するためのオプションを検討することもお勧めします。筆者はこのブログで紹介したすべてのコードを GitHubへ公開しています。さらなるテストやフィードバックに基づいて改善点があれば更新していきます。もっと大きな整数や小数が必要な場合は、Rudy’s libraryをご覧ください。